In this blog post, I will try to explain in simplest words possible as to what happens to a building during an earthquake.
Imagine this: You are travelling in a car which I am driving. I applied a sudden brake. You will experience a serious "jerk" and most probably curse me after that. But that sudden "jerk" also called as deceleration is experienced because your body changed the velocity from 100 feet/second to dead zero in 3 seconds. That is equivalent to gravitational acceleration applied in horizontal direction. This is called inertial force. There was a change in state of motion of your body.
"A body at rest stays at rest and a body in motion stays in motion unless an external force is applied to change the state of body" - Newton's first law of motion.
A force experienced by a body is equal to:
Force = Mass x Acceleration
When earth shakes, it gives these impulses at the base of the building. Let us look at an acceleration time history. (A record showing the ground acceleration plotted against time)
The bottom graph in above image shows the intensity of earthquakes (Arias Intensity) and the region in which there is a steep slope defines the region of strong shaking. Now if the building that you have designed is not able to handle this steep energy curve, that is if it cannot handle the rate seismic energy entering into the building, then it will collapse. But we know that we cannot design a building to store this much amount of energy, so we have to design it in such a way that it dissipates this energy entering into the building. But the major question is how can we dissipate energy from the building?
Before moving to energy dissipation, let us talk about how a force can be looked as energy absorbed into the system. Whenever a force acts on an object, the force deforms that particular object which means that object experiences different strains. This force times the amount of deformation is called strain energy. Similarly if building dissipates energy between two oscillations, it is called damping energy and so on. So during an earthquake motion, seismic energy is entering into the building system and the this energy that is entered is dissipated from the building in terms of inelastic deformations, elastic deformations and damping.
Seismic Energy = Inelastic energy + Strain Energy + Modal Damping + Rayleigh Damping + Additional Viscous Dampers
Let us talk about all these energies and focus on the most critical part of the above equation.
1. Strain Energy
Strain energy is the elastic deformation energy. This means that the elements in the building will stay elastic and deform within the elastic zone. The principle of superposition will be applicable and stress will be proportional to strain. But the amount of earthquake energy dissipated by this energy is very less. If you are thinking why, then here is the answer. As I said that the strain energy is just the elastic zone of the members experiencing lateral forces, the energy will be 1/2*Force*Deformation. Now even if the members each the yield capacity the elastic deformations at that yield capacities are very low. Take a look at graph below:
Area under the curve: Elastic strains and plastic strains
As you can see from the image above, that the elastic strain energy zone is very small. That is it starts from 1 and reaches up to point 2. Thus the area under that curve is the energy absorbed by member. This is the reason why even if we have so many members but the the strain energy dissipation during earthquakes is so low as compared to other energy dissipation.
2. Damping Energy
As discussed in our previous blog Response Spectrum Analysis, we talked about damping. Damping is the energy released from the system. Take a tuning fork or a scale in your hand, hold it tight and give it an impact. At the beginning of the impact the scale will start oscillating violently, but soon the vibrations will lower down and eventually come to stop. Now one might wonder where did all the energy go? Because the total input energy should be equal to the total output energy. So over here, majority of the energy dissipated in the form of damping energy. How can I say that? Well, when you gave a hit to the scale as soon as it started oscillating, your hand started shaking as well as the bond between you hand and the scale was not entirely rigid. So the scale started losing most of its energy at the scale-hand interaction. Apart from this your hand also started shaking which results in some more energy dissipation.
Damping is a kind of black hole for structural engineering. We know that the faster a building oscillates, the faster it will dissipate energy as damping energy released is directly proportional to the velocity of object moving. But we don't know how much amount of damping coefficient each building can provide. It can range from 1.5% for tall buildings to 5% for short concrete buildings. So a shorter building can quickly dissipate its energy as compared to a taller building. A tall building goes under many free oscillations after an earthquake ends while a shorter building stops oscillating quite quickly as soon as the earthquake ends. Just because a taller building has lower damping coefficient and they have longer periods. A tall building can have a period ranging from 4 seconds to as high as 10 seconds. While a short building has a period of less than 1 second. Now how does it matter? Damping energy is released within each cycle.
let us say you are measuring energy released from the building in 20 seconds. The two building that we are placing under the microscope has the same damping constant but different periods, one has a period of 1 second while the other has a period of 5 seconds. Now the building with a period of 1 second will oscillate 20 times while the building with 5 second period will oscillate 4 times. Now let us say the energy released is 5% in each cycle of the total energy in building. Then definitely the building with more cycles will release energy more quickly. Of course there are many different parameters into consideration but this the simplest way I can explain as how come a shorter building stops vibrating more quickly as compared to a tall building.
The damping energy that is released is in for of cracking of concrete or banging of two members against each other, banging of wall against a structural member and what not. We will go into the details of damping into another article.
3. Additional Viscous Dampers
Sometimes when the building is too sensitive to small forces say for example wind, then we install additional dampers to attain higher amount of damping. This damping absorbs a lot of energy from the structure. You can tune the damping as per your wish say 2% or 3% or even 5% additional to what the building can provide. These are dashpots that are installed in the form of a brace or as a link between the beam.
2. Damping Energy
As discussed in our previous blog Response Spectrum Analysis, we talked about damping. Damping is the energy released from the system. Take a tuning fork or a scale in your hand, hold it tight and give it an impact. At the beginning of the impact the scale will start oscillating violently, but soon the vibrations will lower down and eventually come to stop. Now one might wonder where did all the energy go? Because the total input energy should be equal to the total output energy. So over here, majority of the energy dissipated in the form of damping energy. How can I say that? Well, when you gave a hit to the scale as soon as it started oscillating, your hand started shaking as well as the bond between you hand and the scale was not entirely rigid. So the scale started losing most of its energy at the scale-hand interaction. Apart from this your hand also started shaking which results in some more energy dissipation.
Figure showing undamped oscillation
Damping is a kind of black hole for structural engineering. We know that the faster a building oscillates, the faster it will dissipate energy as damping energy released is directly proportional to the velocity of object moving. But we don't know how much amount of damping coefficient each building can provide. It can range from 1.5% for tall buildings to 5% for short concrete buildings. So a shorter building can quickly dissipate its energy as compared to a taller building. A tall building goes under many free oscillations after an earthquake ends while a shorter building stops oscillating quite quickly as soon as the earthquake ends. Just because a taller building has lower damping coefficient and they have longer periods. A tall building can have a period ranging from 4 seconds to as high as 10 seconds. While a short building has a period of less than 1 second. Now how does it matter? Damping energy is released within each cycle.
Figure showing damped oscillation describing energy loss in every cycle
let us say you are measuring energy released from the building in 20 seconds. The two building that we are placing under the microscope has the same damping constant but different periods, one has a period of 1 second while the other has a period of 5 seconds. Now the building with a period of 1 second will oscillate 20 times while the building with 5 second period will oscillate 4 times. Now let us say the energy released is 5% in each cycle of the total energy in building. Then definitely the building with more cycles will release energy more quickly. Of course there are many different parameters into consideration but this the simplest way I can explain as how come a shorter building stops vibrating more quickly as compared to a tall building.
The damping energy that is released is in for of cracking of concrete or banging of two members against each other, banging of wall against a structural member and what not. We will go into the details of damping into another article.
3. Additional Viscous Dampers
Sometimes when the building is too sensitive to small forces say for example wind, then we install additional dampers to attain higher amount of damping. This damping absorbs a lot of energy from the structure. You can tune the damping as per your wish say 2% or 3% or even 5% additional to what the building can provide. These are dashpots that are installed in the form of a brace or as a link between the beam.
Viscous dampers installed in a building in diagonal action
These dampers have critical damping coefficient and the maximum force that they can resist. Any additional force will not be resisted it will end up deforming more than specified. So it becomes critical as how you model these dampers. Generally in case of modelling you should assign a spring and a damper in series where spring will reflect the stiffness of the member and damper will reflect the damping coefficient. You add these dampers at multiple locations to get up to the desired damping coefficient of the entire building.
All the above mentioned energies contribute to majority of energy dissipation in a structure. I am not providing a range as the remaining energy dissipation is in the form of inelastic energy dissipated from coupling beams, shear wall hinging at the base or in case of moment frames hinging at the beam ends or in case of buckling restrained brace frames in the form of tension and compression of the braces and the inelastic cycle it goes through. It becomes extremely important to dissipate energy in terms of this inelasticity as a building which lacks in this zone generally fails or collapses during an earthquake. Yes there are many more concepts to instability and there are many more failure modes too, but right now I am just touching base with a generalized concept of inelastic behavior. When we looked at Arias intensity curve above, we saw a sudden spike, this spike varies between earthquakes and the the slope of the spike can be different in different earthquakes. If the slope is low than it means that earthquake has low energy input per second and the building has more chances of survival. But if the spike is very steep that means high energy input per second into the building, then only well detailed and well analyzed and designed buildings has the chances of survival and the rest will definitely collapse. So in order to make sure that the energy dissipation capacity of the building is always greater than this energy demand, we have to provide inelastic energy dissipation sources as strain energy is not going to help us in any way. So lets talk about inelastic energy dissipation.
4. Ductility
Ductility is known as the ability of material to deform beyond its elastic yield limit into the plastic zone. I have already published a blog on elasticity vs ductility which you can find here.
Ductility is important to achieve the inelastic zone and in inelastic energy dissipation. If the material is not ductile then it does not have the stamina to go into hundreds of inelastic cycles in case of an earthquake. These cycles look something like this:
Ductility is important to achieve the inelastic zone and in inelastic energy dissipation. If the material is not ductile then it does not have the stamina to go into hundreds of inelastic cycles in case of an earthquake. These cycles look something like this:
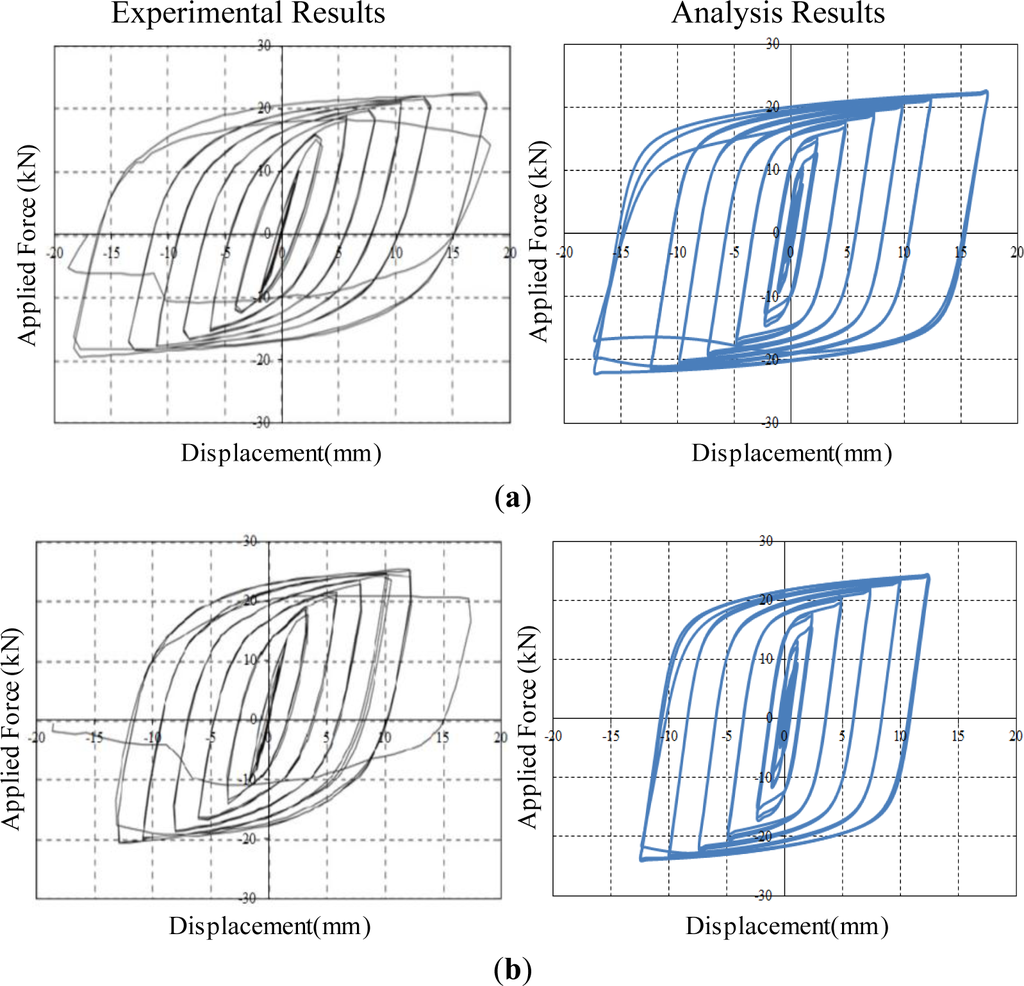
The image above shows the force deformation relationship of a buckling restrained brace. These braces can work without failing in compression (buckling restrained) and so they can offer high strength as well as ductility in tension as well as compression. As you can see the area under the curve in the initial elastic zone which goes up to a displacement of 1 millimeter is very insignificant as compared to the rest of the area under the curve which shows that the braces can work up to 15 millimeters of displacement quite easily without losing its strength. This is the beauty of ductility. Apart from damping energy released the next maximum source of energy dissipation is the ductility in the lateral force resisting system. The energy dissipated in the form of these inelastic hysteresis loops is generally of the order of 15-30% of the strain energy itself. That is significant source of energy dissipation just by making sure that the structure is ductile enough. Isn't that pretty amazing?
What are the members that contribute to these ductile energy dissipation?
1. Shear wall base or more commonly known as shear wall hinge zone.
2. Coupling beams in coupled shear walls
3. Beams in a moment frame
4. Buckling restrained braces in case of a braced frame system
5. Conventional braces in case of a braced frame system
6. Link beams in case of eccentric braced frame system
How to make sure that the structure is ductile? Oh boy, it is a vast topic. I am planning to put a next blog post soon which will be related to "Ductile design of structure in seismic zone".
I hope you enjoyed a little introduction to what happens to a building during an earthquake and how energy is pumped into the building and how building works to dissipate that energy. Remember this was a very generalized post so do not take the numbers seriously. Make sure you do your research specific to your project because all the projects are different in case of structural engineering.
Thank you. Have a nice day.






"Ductile design of structure in seismic zone". dear sir eagerly waiting for this topic
ReplyDelete